Les modalités de calcul précises du coefficient sont renvoyées à un décret, mais il ressort des discussions au Sénat et à l’Assemblée qu’elles seront fortement inspirées de celles utilisées pour la dotation forfaitaire des communes.
D’un coefficient 1 jusqu’à 500 habitant jusqu’à 2 à partir de 200 000 habitants, en passant par 1,5 pour 10 000 habitant. Une représentation graphique nous montre une progression surtout forte sur les plus petites entités puis un aplatissement de la courbe au-delà. En apparence, ce mécanisme ne devrait donc pas être trop défavorable aux grandes entités, au même titre que les strates qu’il remplace.
Mais les apparences sont parfois trompeuses et un examen approfondi permet de relever un véritable contresens :
- Dans le cas de la dotation forfaitaire des communes, ce coefficient logarithmique vient corriger un montant uniforme par habitant, considérant qu’une commune de 200 000 habitants, au vu de ses charges, doit percevoir 2 fois plus par tête qu’une commune de 500 habitants. La forte progressivité de l’échelle logarithmique permet donc de maximiser la dotation des communes de plus de 10 000 habitants.
- Dans le cas du prélèvement Fpic et du calcul du potentiel financier agrégé (PFIA) c’est exactement le contraire : le PFIA des grandes entités est déjà en moyenne plus élevé que celui des petites (ce qui justifiait la logique des strates) et en lui affectant un coefficient multiplicateur jouant dans le même sens, on accentue la richesse théorique des grandes entités et donc leur écart à la moyenne qui détermine si elles seront prélevées ou pas.
Prenons un exemple pour illustrer ce phénomène : plaçons-nous au seuil de prélèvement soit 90 % du PFIA moyen, qui s’élevait à 993 € dans les simulations fournies par le Gouvernement, soit un PFIA de 893 €/habitant.Avec le mécanisme des strates, toute entité comportant moins de 50 000 habitants aurait subi un prélèvement (les PFIA moyens des strates basses étant plus faibles) ; à l’inverse au-delà de 50 000 habitants, pas de prélèvement.
Substituer l’effet taille à l’effet richesse – Avec le coefficient logarithmique retenu par les Parlementaires, toutes les entités disposant de ce niveau de PFIA seraient prélevées, y compris les plus peuplées, le prélèvement augmentant en outre avec la taille de l’entité. En réalité l’application du coefficient logarithmique revient donc à substituer l’effet taille à l’effet richesse : le Fpic n’est plus un fond de péréquation des « riches » vers les « pauvres » mais des « grands » vers les « petits ».
En reprenant les simulations fournies par le Gouvernement en novembre dernier (et dont les données de bases comme le PFIA restent d’actualité) ce glissement est confirmé :
- Toutes les entités de plus de 200 000 habitants seraient désormais prélevées, contre 19 sur 42 dans la version initiale du Fpic.
- A l’inverse, en deçà de 10 000 habitants, le nombre d’entités prélevées passerait de 1 236 dans la version initiale à 801 dans la version actuelle
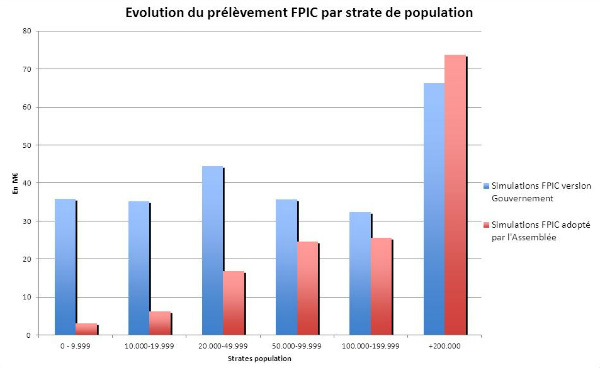
En simulant les masses financières prélevées, on relève qu’en dépit de la diminution du montant global de 250 M€ à 150 M€ du Fpic en 2012, les entités de plus de 200 000 habitants seraient davantage prélevées, tandis que le prélèvement total sur les entités de moins de 10 000 habitants serait divisé par plus de 10 !
Cela résulte d’un effet secondaire des nouvelles modalités de calcul : en prélevant davantage de grandes entités le prélèvement par habitant diminue (effet renforcé par la diminution du prélèvement global pour 2012), ce qui limite mécaniquement les prélèvements en valeur absolue des plus petites entités et majore celui des plus grandes.
Au regard des objectifs initiaux du Fpic, le choix finalement effectué pour calculer le prélèvement relève bien du contresens, sauf à imaginer que les parlementaires ont sciemment décidé de ponctionner principalement les grandes communautés et communes au bénéfice des petites.
Christophe Michelet, Partenaires Finances Locales
Cet article est en relation avec les dossiers
- Budget 2012 : les collectivités au régime sec
- FPIC : la péréquation du bloc local continue sa montée en puissance
Thèmes abordés